В этом материале разберу несколько случаев параметризации кривых траекторий. Зачастую для них недостаточно просто указать радиус закругления, иногда приходится вводить больше вспомогательных переменных. Разберу на примерах.
Фигура 1: простой случай с закруглением
Начнём с самого обычного закругления. Две прямые линии подходят друг к другу под 90° и соединяются по радиусу заданного значения. В этом случае всё просто: строите эти линии, берёте инструмент «Дуга сопряжения» и с его помощью образуете дугу. Далее её нужно выделить, появится временный радиальный размер, преобразуйте его в постоянный.
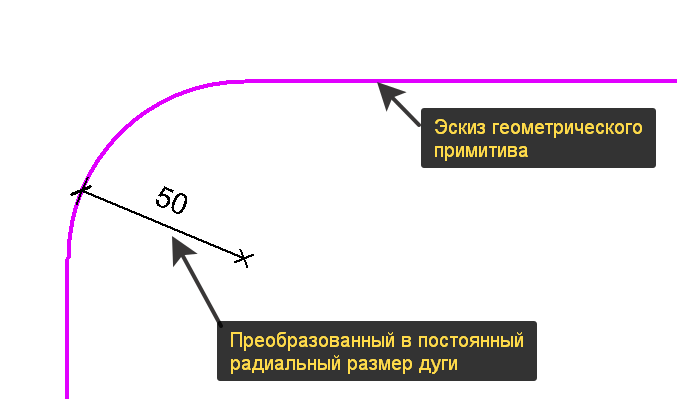
Если радиус может меняться, то нужно назначить на размер параметр и менять через параметр. Даже если радиус не меняется, всё равно создавайте размер, это гарантия того, что при перестроениях закругление не сломается.
Фигура 2: усеченный конус с закруглением сверху
Следующая задача — модификация первой. Теперь наши линии смыкаются с закруглением, но угол между ними больше 90°. Как пример — усеченный конус с закруглением на верхней грани, например колпачок термоголовки или какого-нибудь клапана. Здесь построения будут сложнее, распишу по этапам.
Создаём эскиз без скругления, привязываем прямые линии к опорным плоскостям. У линии под углом привязываем нижнюю точку к пересечению опорных плоскостей. Для этого нужно взять инструмент выравнивание, выделить опорную плоскость, навести курсор на точку и нажать Таб, чтобы она подсветилась.
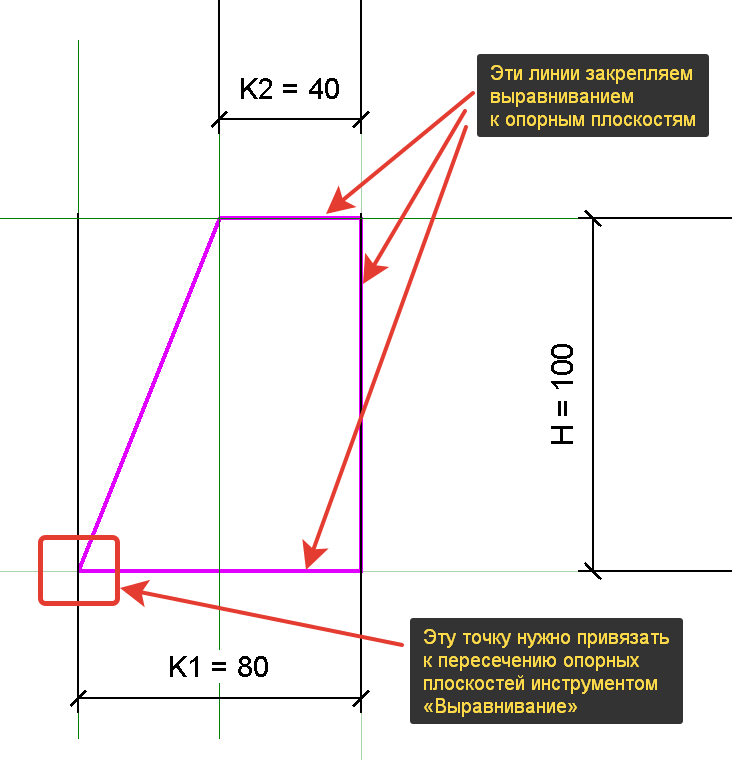
Теперь формируем закругление дугой сопряжения, можно пока выбрать любой радиус, чтобы было удобно работать. Сделали дугу, теперь нужно «оторвать» от неё верхнюю горизонтальную линию — у дуги должен быть один открытый конец. Вот так:
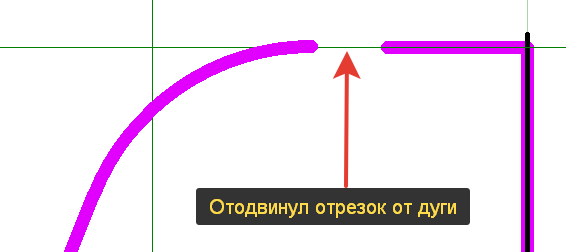
Теперь выделяем дугу, у неё появятся временные размеры, радиус и угол дуги. Оба преобразовываем в постоянные размеры и вешаем параметры. Значение радиуса будете вносить то, которое нужно, а угол дуги нужно вычислить. Этот угол равен углу в основании треугольника, который образовывает наш эскиз. Туда тоже нужно поставить угловой размер и назначить параметр с углом дуги.
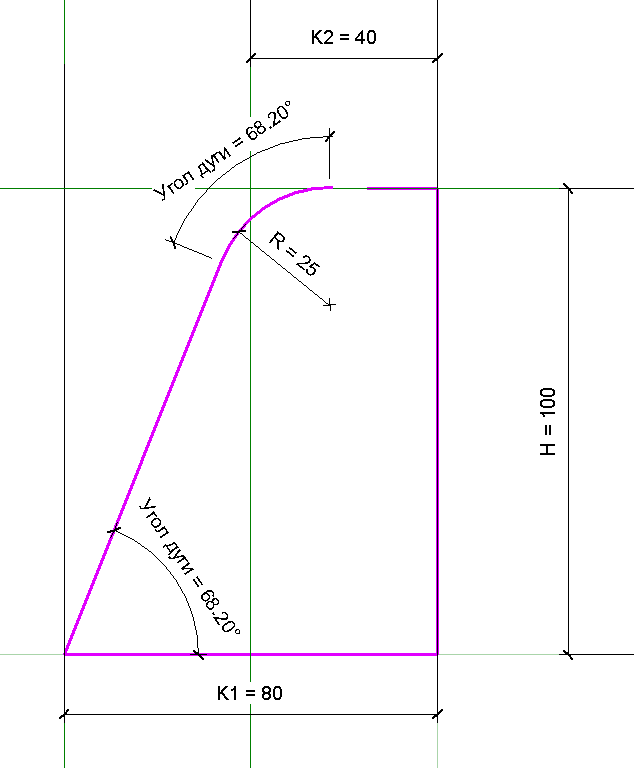
После этого можно снова соединить верхний отрезок и дугу. Осталось добавить формулу для вычисления угла и всё готово. Формула такая, имена переменных замените на имена из вашего семейства:
Угол дуги = atan(H / (K1-K2))Следите, чтобы радиус закругления не был слишком большим, иначе прямая линия может обратиться в ноль или отрицательное значение, в этом случае Ревит сломает геометрию и выдаст ошибку.
Фигура 3: плавный переход из окружности в прямую
Столкнулся с ней, когда делал на заказ семейства подвесных опор трубопроводов с хомутами на концах. Хомут плавно переходит через радиус в прямую площадку, где хомуты прикручивают друг к другу.

В тот раз у меня не получилось решить проблему, хотя она несложная, как кажется теперь.
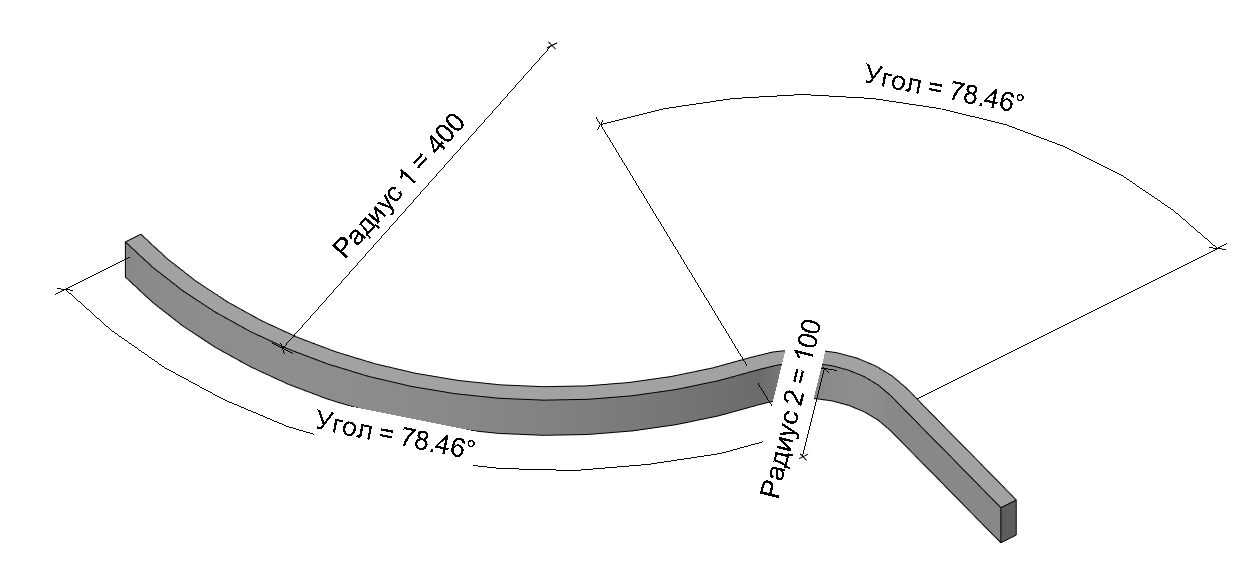
Сразу покажу запараметризированную траекторию, в ней мы также сначала строим большую полуокружность и прямую линию, а затем их стык скругляем дугой сопряжения. После этого получается две дуги и прямая линия. Дуги нужно оторвать друг от друга, преобразовать временные угловые меры и радиусы в постоянные и задать углам формулы. Ещё одна формула нужна для смещения плоскости привязки центра малой дуги.
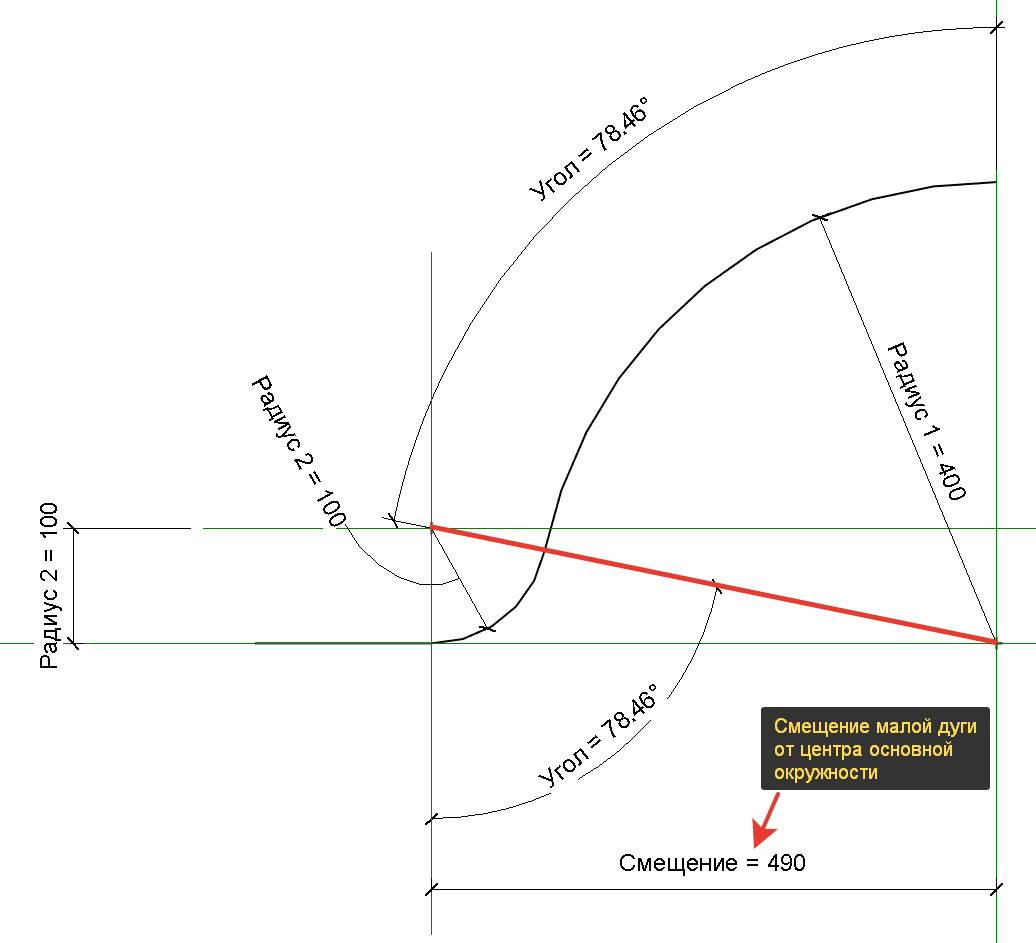
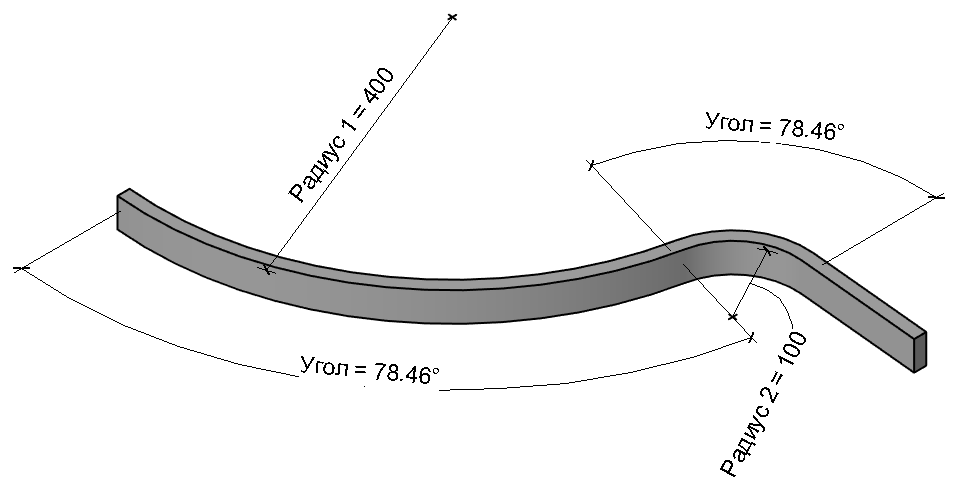
Формула для определения угла:
acos(Радиус 2 / (Радиус 1 + Радиус 2))Формула для определения смещения:
(Радиус 2 + Радиус 1) * sin(Угол)После этого можно формировать сдвиг по траектории, она будет меняться вслед за параметрами без поломок, если не перебарщивать со значениями.


